Simple Traffic Light Plc Program Free Download Programs
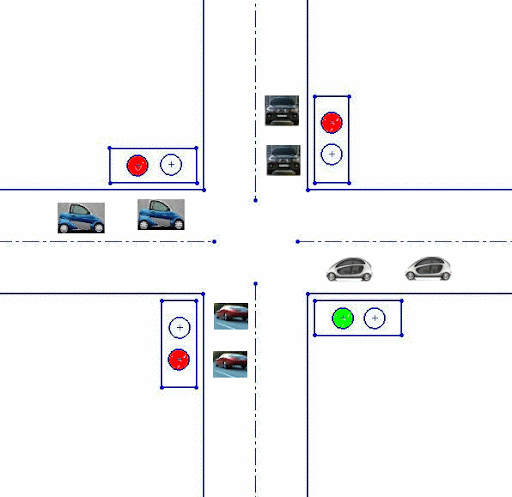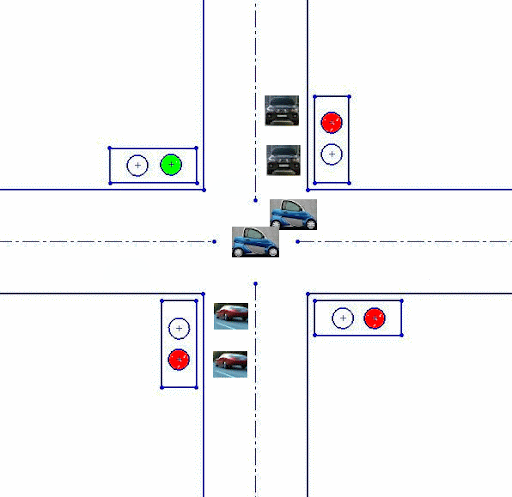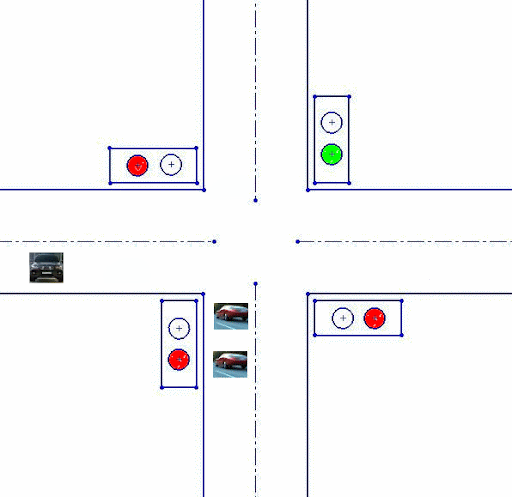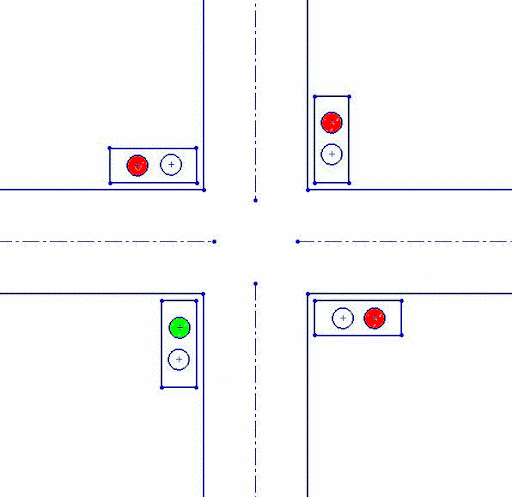
No patent liability is assumed by Rockwell Automation with respect to use of information, circuits, equipment, or software described in. Basic PLC Programming with Micro800™ Controller Family. Before you can download an application to the controller, you must build it to verify that there are no errors with the. Development of a traffic light control system using PLC (Programmable Logic Controller) is the title of this project. This project is divided into two parts which are hardware and software. The hardware part for this project is a model of four way junction of a traffic light. Each lane has two limits switch (input) function as a sensor.
University Of Craiova
In the matrix A [ i , j ] put the System of N-Equation.
In the vector b put the solutions
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Example 1: Linear System 3 equation (X,Y,Z)
3 X + 2 Y - Z = 10
- X + Y + Z = -2
2 X - Y + 2 Z = -6
3 2 -1 10
X -1 + Y 1 + Z 1 = -2
2 -1 2 -6
Matrix A :=
Matrix[1,1]= 3 ; Matrix[1,2]= 2 ; Matrix[1,3]= -1
Matrix[2,1]= -1 ; Matrix[2,2]= 1 ; Matrix[2,3]= -2
Matrix[3,1]= 2 ; Matrix[3,2]= -1 ; Matrix[3,3]= -6
Vector b:=
Vector[1] =10 ; Vector[2] = -2 ; Vector[3] = -6 ;
Solution :=
Solution [1] := 1.0 ; Solution [2] := 2.0 ; Solution [3] := -3.0 ;
X = 1 ; Y = 2 ; Z = -3
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Example 2: Linear System 5 equation for resolve Polynomial 4th grade
exampl. Polynomial whit 5 points:
P0(-1,-1) ;
P1( 1, 3) ;
P2( 5, 3.5) ;
P3( 6, 4.5) ;
P4( 7, 7) ;
Write in the Matrix A [ i, j ]
Matrix A :=
Matrix[1,1]= (-1)^4 ; Matrix[1,2]= (-1)^3 ; Matrix[1,3]= (-1)^2 ; Matrix[1,4]= (-1) ; Matrix[1,5]=1;
Matrix[2,1]= (1)^4 ; Matrix[2,2]= (1)^3 ; Matrix[2,3]= (1)^2 ; Matrix[2,4]= (1) ; Matrix[2,5]=1;
Matrix[3,1]= (5)^4 ; Matrix[3,2]= (5)^3 ; Matrix[3,3]= (5)^2 ; Matrix[3,4]= (5) ; Matrix[3,5]=1;
Matrix[4,1]= (6)^4 ; Matrix[4,2]= (6)^3 ; Matrix[4,3]= (6)^2 ; Matrix[4,4]= (6) ; Matrix[4,5]=1;
Matrix[5,1]= (7)^4 ; Matrix[5,2]= (7)^3 ; Matrix[5,3]= (7)^2 ; Matrix[5,4]= (7) ; Matrix[5,5]=1;
Write in the Vector [ ]
Vector b:=
Vector[1] = -1 ; Vector[2] = 3 ; Vector[3] = 3.5 ; Vector[4] = 4.5 ; Vector[5] = 7
Solutions :=
Solution [1] := 3.27380234e-003 ; Solution [2] := 0.03363105;
Solution [3] := -0.56577414 ; Solution [4] := 1.966369 ;
Solution [5] := 1.5625005
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Example 3: Linear System 6 equation for resolve Polynomial 5th grade
example. Mototion Interpolation whit Polynomial
whit 2 Points :
P0 (Time0, Position 0) Start point whit (Velocity 0, Acceleration 0)
P1 (Time1, Position 1) End point whit (Velocity 1, Acceleration 1)
Write in the Matrix A [ i, j ]
Matrix A :=
X0 = time0 ; X1 = time1
Row1 X0 ^5 + X0 ^4 + X0 ^3 + X0 ^2 + X0 + 1 (Position P0)
Row2 5 * X0 ^4 + 4 * X0 ^3 + 3 * X0 ^2 + 2 * X0 + 1 + 0 (Velocity P0)
Row3 20 * X0 ^3 + 12 * X0 ^2 + 6 * X0 + 2 + 0 + 0 (Acceleration P0)
Row4 X1 ^5 + X1 ^4 + X1 ^3 + X1 ^2 + X1 + 1 (Position P1)
Row5 5 * X1 ^4 + 4 * X1 ^3 + 3 * X1 ^2 + 2 * X1 + 1 + 0 (Velocity P1)
Row6 20 * X1 ^3 + 12 * X1 ^2 + 6 * X1 + 2 + 0 + 0 (Acceleration P1)
Vector b:=
Vector[1] = Position P0 ; Vector[2] = Velocity P0 ; Vector[3] = Acceleration P0 ;
Vector[4] = Position P1 ; Vector[5] = Velocity P1 ; Vector[6] = Acceleration P1 ;
Interpolation Polynomial Position :=
Position := s1* t^5 + s2* t^4 +s3* t^3 + s4* t^2 + s5* t + s6;
In the vector b put the solutions
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Example 1: Linear System 3 equation (X,Y,Z)
3 X + 2 Y - Z = 10
- X + Y + Z = -2
2 X - Y + 2 Z = -6
3 2 -1 10
X -1 + Y 1 + Z 1 = -2
2 -1 2 -6
Matrix A :=
Matrix[1,1]= 3 ; Matrix[1,2]= 2 ; Matrix[1,3]= -1
Matrix[2,1]= -1 ; Matrix[2,2]= 1 ; Matrix[2,3]= -2
Matrix[3,1]= 2 ; Matrix[3,2]= -1 ; Matrix[3,3]= -6
Vector b:=
Vector[1] =10 ; Vector[2] = -2 ; Vector[3] = -6 ;
Solution :=
Solution [1] := 1.0 ; Solution [2] := 2.0 ; Solution [3] := -3.0 ;
X = 1 ; Y = 2 ; Z = -3
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Example 2: Linear System 5 equation for resolve Polynomial 4th grade
exampl. Polynomial whit 5 points:
P0(-1,-1) ;
P1( 1, 3) ;
P2( 5, 3.5) ;
P3( 6, 4.5) ;
P4( 7, 7) ;
Write in the Matrix A [ i, j ]
Matrix A :=
Matrix[1,1]= (-1)^4 ; Matrix[1,2]= (-1)^3 ; Matrix[1,3]= (-1)^2 ; Matrix[1,4]= (-1) ; Matrix[1,5]=1;
Matrix[2,1]= (1)^4 ; Matrix[2,2]= (1)^3 ; Matrix[2,3]= (1)^2 ; Matrix[2,4]= (1) ; Matrix[2,5]=1;
Matrix[3,1]= (5)^4 ; Matrix[3,2]= (5)^3 ; Matrix[3,3]= (5)^2 ; Matrix[3,4]= (5) ; Matrix[3,5]=1;
Matrix[4,1]= (6)^4 ; Matrix[4,2]= (6)^3 ; Matrix[4,3]= (6)^2 ; Matrix[4,4]= (6) ; Matrix[4,5]=1;
Matrix[5,1]= (7)^4 ; Matrix[5,2]= (7)^3 ; Matrix[5,3]= (7)^2 ; Matrix[5,4]= (7) ; Matrix[5,5]=1;
Write in the Vector [ ]
Vector b:=
Vector[1] = -1 ; Vector[2] = 3 ; Vector[3] = 3.5 ; Vector[4] = 4.5 ; Vector[5] = 7
Solutions :=
Solution [1] := 3.27380234e-003 ; Solution [2] := 0.03363105;
Solution [3] := -0.56577414 ; Solution [4] := 1.966369 ;
Solution [5] := 1.5625005
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Example 3: Linear System 6 equation for resolve Polynomial 5th grade
example. Mototion Interpolation whit Polynomial
whit 2 Points :
P0 (Time0, Position 0) Start point whit (Velocity 0, Acceleration 0)
P1 (Time1, Position 1) End point whit (Velocity 1, Acceleration 1)
Write in the Matrix A [ i, j ]
Matrix A :=
X0 = time0 ; X1 = time1
Row1 X0 ^5 + X0 ^4 + X0 ^3 + X0 ^2 + X0 + 1 (Position P0)
Row2 5 * X0 ^4 + 4 * X0 ^3 + 3 * X0 ^2 + 2 * X0 + 1 + 0 (Velocity P0)
Row3 20 * X0 ^3 + 12 * X0 ^2 + 6 * X0 + 2 + 0 + 0 (Acceleration P0)
Row4 X1 ^5 + X1 ^4 + X1 ^3 + X1 ^2 + X1 + 1 (Position P1)
Row5 5 * X1 ^4 + 4 * X1 ^3 + 3 * X1 ^2 + 2 * X1 + 1 + 0 (Velocity P1)
Row6 20 * X1 ^3 + 12 * X1 ^2 + 6 * X1 + 2 + 0 + 0 (Acceleration P1)
Vector b:=
Vector[1] = Position P0 ; Vector[2] = Velocity P0 ; Vector[3] = Acceleration P0 ;
Vector[4] = Position P1 ; Vector[5] = Velocity P1 ; Vector[6] = Acceleration P1 ;
Interpolation Polynomial Position :=
Position := s1* t^5 + s2* t^4 +s3* t^3 + s4* t^2 + s5* t + s6;
Hong Kong Environmental Protection Department
In the matrix A [ i , j ] put the System of N-Equation.
In the vector b put the solutions
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Example 1: Linear System 3 equation (X,Y,Z)
3 X + 2 Y - Z = 10
- X + Y + Z = -2
2 X - Y + 2 Z = -6
3 2 -1 10
X -1 + Y 1 + Z 1 = -2
2 -1 2 -6
Matrix A :=
Matrix[1,1]= 3 ; Matrix[1,2]= 2 ; Matrix[1,3]= -1
Matrix[2,1]= -1 ; Matrix[2,2]= 1 ; Matrix[2,3]= -2
Matrix[3,1]= 2 ; Matrix[3,2]= -1 ; Matrix[3,3]= -6
Vector b:=
Vector[1] =10 ; Vector[2] = -2 ; Vector[3] = -6 ;
Solution :=
Solution [1] := 1.0 ; Solution [2] := 2.0 ; Solution [3] := -3.0 ;
X = 1 ; Y = 2 ; Z = -3
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Example 2: Linear System 5 equation for resolve Polynomial 4th grade
exampl. Polynomial whit 5 points:
P0(-1,-1) ;
P1( 1, 3) ;
P2( 5, 3.5) ;
P3( 6, 4.5) ;
P4( 7, 7) ;
Write in the Matrix A [ i, j ]
Matrix A :=
Matrix[1,1]= (-1)^4 ; Matrix[1,2]= (-1)^3 ; Matrix[1,3]= (-1)^2 ; Matrix[1,4]= (-1) ; Matrix[1,5]=1;
Matrix[2,1]= (1)^4 ; Matrix[2,2]= (1)^3 ; Matrix[2,3]= (1)^2 ; Matrix[2,4]= (1) ; Matrix[2,5]=1;
Matrix[3,1]= (5)^4 ; Matrix[3,2]= (5)^3 ; Matrix[3,3]= (5)^2 ; Matrix[3,4]= (5) ; Matrix[3,5]=1;
Matrix[4,1]= (6)^4 ; Matrix[4,2]= (6)^3 ; Matrix[4,3]= (6)^2 ; Matrix[4,4]= (6) ; Matrix[4,5]=1;
Matrix[5,1]= (7)^4 ; Matrix[5,2]= (7)^3 ; Matrix[5,3]= (7)^2 ; Matrix[5,4]= (7) ; Matrix[5,5]=1;
Write in the Vector [ ]
Vector b:=
Vector[1] = -1 ; Vector[2] = 3 ; Vector[3] = 3.5 ; Vector[4] = 4.5 ; Vector[5] = 7
Solutions :=
Solution [1] := 3.27380234e-003 ; Solution [2] := 0.03363105;
Solution [3] := -0.56577414 ; Solution [4] := 1.966369 ;
Solution [5] := 1.5625005
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Example 3: Linear System 6 equation for resolve Polynomial 5th grade
example. Mototion Interpolation whit Polynomial
whit 2 Points :
P0 (Time0, Position 0) Start point whit (Velocity 0, Acceleration 0)
P1 (Time1, Position 1) End point whit (Velocity 1, Acceleration 1)
Write in the Matrix A [ i, j ]
Matrix A :=
X0 = time0 ; X1 = time1
Row1 X0 ^5 + X0 ^4 + X0 ^3 + X0 ^2 + X0 + 1 (Position P0)
Row2 5 * X0 ^4 + 4 * X0 ^3 + 3 * X0 ^2 + 2 * X0 + 1 + 0 (Velocity P0)
Row3 20 * X0 ^3 + 12 * X0 ^2 + 6 * X0 + 2 + 0 + 0 (Acceleration P0)
Row4 X1 ^5 + X1 ^4 + X1 ^3 + X1 ^2 + X1 + 1 (Position P1)
Row5 5 * X1 ^4 + 4 * X1 ^3 + 3 * X1 ^2 + 2 * X1 + 1 + 0 (Velocity P1)
Row6 20 * X1 ^3 + 12 * X1 ^2 + 6 * X1 + 2 + 0 + 0 (Acceleration P1)
Vector b:=
Vector[1] = Position P0 ; Vector[2] = Velocity P0 ; Vector[3] = Acceleration P0 ;
Vector[4] = Position P1 ; Vector[5] = Velocity P1 ; Vector[6] = Acceleration P1 ;
Interpolation Polynomial Position :=
Position := s1* t^5 + s2* t^4 +s3* t^3 + s4* t^2 + s5* t + s6;
In the vector b put the solutions
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Example 1: Linear System 3 equation (X,Y,Z)
3 X + 2 Y - Z = 10
- X + Y + Z = -2
2 X - Y + 2 Z = -6
3 2 -1 10
X -1 + Y 1 + Z 1 = -2
2 -1 2 -6
Matrix A :=
Matrix[1,1]= 3 ; Matrix[1,2]= 2 ; Matrix[1,3]= -1
Matrix[2,1]= -1 ; Matrix[2,2]= 1 ; Matrix[2,3]= -2
Matrix[3,1]= 2 ; Matrix[3,2]= -1 ; Matrix[3,3]= -6
Vector b:=
Vector[1] =10 ; Vector[2] = -2 ; Vector[3] = -6 ;
Solution :=
Solution [1] := 1.0 ; Solution [2] := 2.0 ; Solution [3] := -3.0 ;
X = 1 ; Y = 2 ; Z = -3
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Example 2: Linear System 5 equation for resolve Polynomial 4th grade
exampl. Polynomial whit 5 points:
P0(-1,-1) ;
P1( 1, 3) ;
P2( 5, 3.5) ;
P3( 6, 4.5) ;
P4( 7, 7) ;
Write in the Matrix A [ i, j ]
Matrix A :=
Matrix[1,1]= (-1)^4 ; Matrix[1,2]= (-1)^3 ; Matrix[1,3]= (-1)^2 ; Matrix[1,4]= (-1) ; Matrix[1,5]=1;
Matrix[2,1]= (1)^4 ; Matrix[2,2]= (1)^3 ; Matrix[2,3]= (1)^2 ; Matrix[2,4]= (1) ; Matrix[2,5]=1;
Matrix[3,1]= (5)^4 ; Matrix[3,2]= (5)^3 ; Matrix[3,3]= (5)^2 ; Matrix[3,4]= (5) ; Matrix[3,5]=1;
Matrix[4,1]= (6)^4 ; Matrix[4,2]= (6)^3 ; Matrix[4,3]= (6)^2 ; Matrix[4,4]= (6) ; Matrix[4,5]=1;
Matrix[5,1]= (7)^4 ; Matrix[5,2]= (7)^3 ; Matrix[5,3]= (7)^2 ; Matrix[5,4]= (7) ; Matrix[5,5]=1;
Write in the Vector [ ]
Vector b:=
Vector[1] = -1 ; Vector[2] = 3 ; Vector[3] = 3.5 ; Vector[4] = 4.5 ; Vector[5] = 7
Solutions :=
Solution [1] := 3.27380234e-003 ; Solution [2] := 0.03363105;
Solution [3] := -0.56577414 ; Solution [4] := 1.966369 ;
Solution [5] := 1.5625005
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Example 3: Linear System 6 equation for resolve Polynomial 5th grade
example. Mototion Interpolation whit Polynomial
whit 2 Points :
P0 (Time0, Position 0) Start point whit (Velocity 0, Acceleration 0)
P1 (Time1, Position 1) End point whit (Velocity 1, Acceleration 1)
Write in the Matrix A [ i, j ]
Matrix A :=
X0 = time0 ; X1 = time1
Row1 X0 ^5 + X0 ^4 + X0 ^3 + X0 ^2 + X0 + 1 (Position P0)
Row2 5 * X0 ^4 + 4 * X0 ^3 + 3 * X0 ^2 + 2 * X0 + 1 + 0 (Velocity P0)
Row3 20 * X0 ^3 + 12 * X0 ^2 + 6 * X0 + 2 + 0 + 0 (Acceleration P0)
Row4 X1 ^5 + X1 ^4 + X1 ^3 + X1 ^2 + X1 + 1 (Position P1)
Row5 5 * X1 ^4 + 4 * X1 ^3 + 3 * X1 ^2 + 2 * X1 + 1 + 0 (Velocity P1)
Row6 20 * X1 ^3 + 12 * X1 ^2 + 6 * X1 + 2 + 0 + 0 (Acceleration P1)
Vector b:=
Vector[1] = Position P0 ; Vector[2] = Velocity P0 ; Vector[3] = Acceleration P0 ;
Vector[4] = Position P1 ; Vector[5] = Velocity P1 ; Vector[6] = Acceleration P1 ;
Interpolation Polynomial Position :=
Position := s1* t^5 + s2* t^4 +s3* t^3 + s4* t^2 + s5* t + s6;